先看拓扑流形的定义：

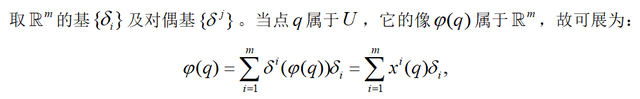
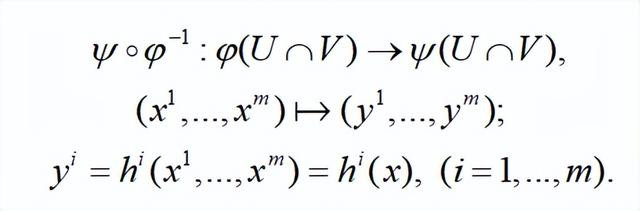
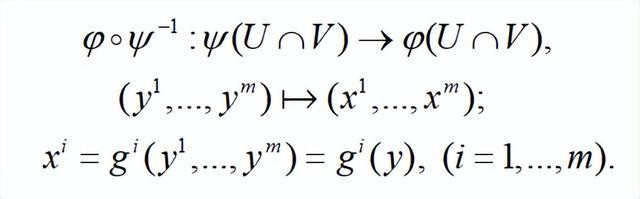
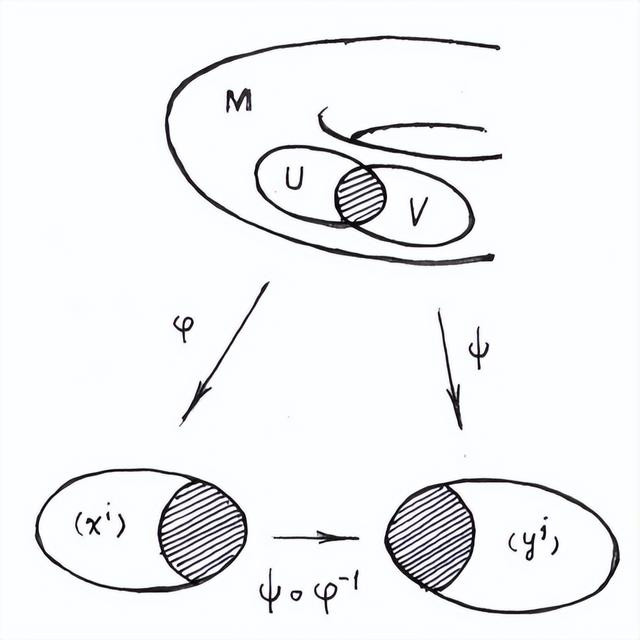
迭置映射（坐标变换）

以上定义的意思大概就是，流形上的每个小块都对应欧氏空间的一个开区间，而欧氏空间是有坐标系的，所以流形上的每个小块都有自己的坐标系，称为坐标卡。

流形上两个小块的相交部分可以映射到欧氏空间的某一块里面，从而使得流形上相交的这两个小块可以粘合起来，也就是所谓的迭置映射。（比如A和B的相交部分可以映射到B块所对应的欧氏空间，则A块剩余的部分也可以）

定义：设 M 和 N 是两个微分流形，ϕα 和ψα 分别是 M 和 N 上的坐标卡。如果ϕα 和ψα 的定义域有交集，那么复合映射

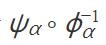
是一个光滑映射，即 C∞ 映射。

应用场景：在微分流形中，迭置映射常用于描述流形在不同坐标卡下的转换关系。例如，假设 M 是一个微分流形，{Oα} 是 M 的一个开覆盖，对于每个开集 Oα，存在一个同胚映射ϕα:Oα→Vα，其中 Vα 是Rn 的一个开子集。如果两个开集Oα 和 Oβ 有交集，那么复合映射

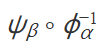
是一个光滑映射，这保证了流形在局部看起来像Rn。

迭置映射反映欧氏空间的小块粘合为流形的局部方式，是局部到整体过渡的基本环节。

迭置映射（或称为坐标变换、映射等）可以将微分流形局部的性质推广到全局，是因为微分流形本身具有局部欧氏空间的性质，且流形的整体结构可以通过局部性质的兼容拼接来描述。

流形是局部具有欧氏空间性质的拓扑空间，即流形上每一点的附近和欧氏空间的一个开集是同胚的。这种局部欧氏空间的性质使得我们可以在流形的每一个局部定义坐标系和微分结构，从而研究流形的局部性质。

然而，微分流形的魅力不仅在于其局部性质，更在于其整体结构。流形的整体结构是通过将局部性质以兼容的方式拼接起来而得到的。这种拼接过程需要依赖于迭置映射，也就是坐标变换。通过迭置映射，我们可以确保流形上不同局部区域的坐标系和微分结构能够平滑地过渡，从而形成一个统一的整体结构。

因此，当我们研究微分流形的全局性质时，可以利用迭置映射将局部性质推广到全局。具体来说，我们可以先在流形的每一个局部区域研究其性质，然后通过迭置映射将这些局部性质拼接起来，得到流形的全局性质。这种方法使得我们能够更加深入地理解微分流形的结构和行为。